K_zone - a new measure of Strikezone Judgment

ã Brian Myers
email: bmyers@zanet.co.za
Johannesburg, South Africa
1 January 1998

The research community has made an enormous contribution to the area of baseball statistics and analysis in recent years. The size of the analyst's ‘toolbox’, as a result, has expanded dramatically. Still, little (or none) of this effort (excluding the now-general acceptance that On-Base-Average (OBA) is the best predictor of a player/team’s ability to score runs) has been directed at assessing strikezone judgment (henceforth referred to as ‘K_zone').Of course, OBA has long been used as a proxy; however, there does not exist, in my judgment, a pure measure of K_zone. Herein, I attempt to provide such a tool.

Ultimately, what one wants to measure is the batter's:

1. ability to draw a walk (strikezone selectivity), and;
2. ability to avoid the strikeout (strikezone command).

For (A), the simple approach would be to measure the frequency with which a batter/team draws a base-on-balls (BB). Hence, (BB / PA), where PA=AB + BB, is used to measure the ability to draw a walk.

The purest measure of (B) would be [(PA – K) / PA]. This returns the frequency with which a player does not strike out. Still, if we want to measure K_zone, it would be better to relate the frequency of Ks to the frequency of BBs. Such a measure would provide a closer approximation of a batter’s ability to work the count. It would also represent a useful proxy for a batter’s handling of high-count situations. Stated plainly, one who walks far more frequently than he strikes out is likely better at working the count. Thus, (BB / K) provides a better measure for (B).

Finally, if we relate each to the league norms, multiply the two terms, and take the nth root (where ‘n’ is the number of terms, in this case two), then we have a useful measure of peer-relative K_zone. Further, since the terms are normalized in this manner, the measure can be used to compare batters and teams across different seasons and eras. By our now-developing method, a player who was average in both respects would produce (A) and (B) terms equal to 1.00, which would result in a K_zone equal to 1.00. As a convenience, we will multiply this preliminary K_zone -rating by 100, so that a player with average level of K_zone would generate a rating of 100 (by corollary, ratings higher than 100 would indicate above average K_zone, and vice-versa).

So our terms are thus:

By multiplying the two terms, taking the square root, and multiplying further by 100, we have a rating useful for comparing players and teams with each other. Our equation is:

K_zone=[ (A) x (B) ] ^1/2 x 100

1. can be interpreted specifically as a measure of walk frequency, a proxy for strikezone selectiveness.
2. measures strikezone command by the proxy of BB per K. K_zoneattempts to measure a batter’s pure relative strikezone judgment, and rests on the assumption that BBs and Ks, when manipulated properly, contain most, if not all, of the information required to make that measurement. Certain other statistics, such as BA with two strikes, allow one to draw inferences about strikezone judgment; however, that data is not widely available, and it also measures other intangibles, such as ability to perform in the clutch. K_zone is a better measure, giving an accurate, pure representation of a batter’s strikezone judgment relative to his peers. A batter with K_zone of 200, for example, has strikezone judgment roughly twice as effective as an average batter. Similarly, K_zone of 50 denotes half the strikezone judgment of an average batter.

Since K_zone is comprised of two normalized ratios, and there is no adjustment for low playing time, K_zone for part-time players can exhibit a very wide variance, and is probably - for this reason - less useful at low levels of PAs. It is possible to adjust K_zone by a factor such as:

MIN ( PA / 400 , 1 )

This would result in full K_zone ratings for full-time players and downward-adjusted ratings for players with less than 400 PA. While this would convey some information, it detracts from the overriding goal. Once any such adjustment is made, the measure no longer says much, if anything, about strikezone judgment. Indeed, while it may be true that a player gets little playing time because he has poor strikezone judgment, it is patently incorrect to assume that a player has poor strikezone judgment because he rides the bench.

Instead, the pool of players for 1998 comparison was limited to those with 400 PA or more.

The Evidence: A Look at 1998

The weighted averages for terms (A) and (B) during 1998, among full-time ML batters, were as follows:

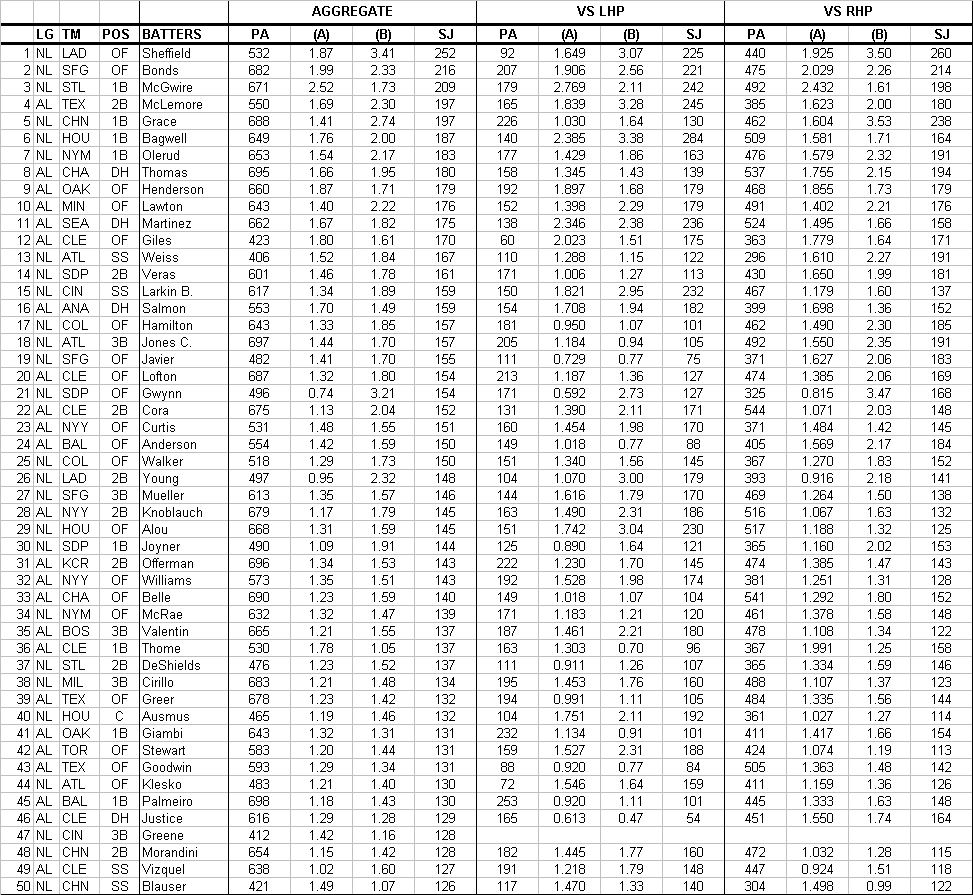
Using these figures as the league averages, we can look at some 1998 player data (note that the LH and RH data for BB, PA, and K do not sum to the TOTAL line, as vs. LH/RH splits were not available for three batters). Of the 206 batters in our pool, 100 achieved average or above average K_zone, and 106 below.

Top 10 batters, K_zone, 1998:

This list looks much as we would expect, dominated by position players located at the left of the defensive spectrum. Note that 9 of the 10 are either DH, 1B, or OF. Note particularly Sheffield’s strikezone command (B). McLemore and Lawton might represent surprises, but each shows good command of the strikezone. In fact, they are two of the most underrated batters in baseball. Lawton shows surprising strikezone judgment for his age, and is likely to enjoy a successful career because of it. Sheffield is simply awesome, ranking 4^th in walk frequency, and 1^st in strikezone command. McGwire was by far the top-ranked player in walk frequency, of course (Bonds was 2^nd, Henderson 3rd), but ranked only 24^th in strikezone command, so his overall ranking is only 3rd.

Worst batters, K_zone, of 1998:

These players have the worst strikezone judgment in the ML. You’ll notice that most of them play defensive positions at the extreme left of the defensive spectrum, which can compensate for poor K_zone. If Coomer moves to 1B, he will likely be afforded little time to improve his K_zone. If he fails to do so, he will probably be out of baseball in 2-3 years. Dunwoody, who plays CF, will quickly wear out his welcome if he does not improve his K_zone. Grissom is running out of time as well; his age will work against him, as he is unlikely to improve much, if at all, at this stage in his career.

It is virtually impossible to develop into an effective hitter for any length of time without developing K_zoneK_zone. Only shortstops, second basemen and catchers are likely to earn any appreciable patience without strong, or at least improving.

K_zonerh and K_zonelh - vs Righties and Lefties

Another interesting way to use K_zone is to examine the best eyes versus lefties/righties, and the differential. In this way, besides the obviously useful splits, we can get an idea of those players with highly disparate strike-zone control. These players might be ideal candidates for a platoon situation. Indeed, we may find that the players sporting the widest differential have the fewest PA's in the group.

Top 10 batters, K_zonerh, 1998:

Much the same group as before, with the surprise additions of Weiss and Anderson. Hamilton and Jones also make the list, which is again dominated by DH, 1B, and OF. Two of the more remarkable numbers to come out of this table are the strikezone command of Sheffield and Grace, each 3.5 x as effective as the average peer.

Top 10 batters, K_zonelh, 1998:

Had McGwire controlled the strike zone as well vs. righties as he did vs. lefties, he might have topped 90 HR. Sheffield, Bonds and McGwire all had excellent K_zoneversus both righties and lefties. Ausmus and Rolen are pleasant surprises… catchers don't often have great K_zone, despite the nature of catching, and Rolen shows promise for a strong career.

K_zone pd - the Platoon Differential

Now, for the K_zone pd (K_zone platoon differential). To measure K_zone pd, I wanted to assess the difference between each batter's K_zonerh and his K_zonelh. Ideally, this measure would give a neutral rating if the batter performs equally, and some non-neutral rating if performance differs. The rating should move further away from zero as performance diverges.

The formula used for K_zone pd is:

K_zone pd=[ 1 - (K_zonelh / K_zonerh) ] x 100

This formula will produce a rating of zero for a player with exactly equivalent K_zonerh and K_zonelh. It will produce a positive number for those who have better K_zonerh, and a negative number for those with better K_zonelh. Moreover, the greater the divergence from zero, the greater the platoon differential.

Intuitively, the comparison of K_zone pd across the player pool is be a less precise science than comparing simple K_zone, since a player who is equally dreadful vs. both will still have a low K_zone pd... drawing only the little-useful conclusion that the hitter's K_zoneis consistently poor. As a fix, I separated the best from the worst, in terms of overallK_zone pd, and then ranked the top 50 by platoon differential (K_zone pd).

Top 10 K_zone pd (lowest differential) among the top 50 by K_zone:

Henderson's remarkable consistency against both righties and lefties marks him as the most successful switch-hitter of our generation, and goes a long way to explaining his durability. Offerman is, like Lawton, underrated, and Giles is developing nicely.

To platoon or not to platoon?

Batters who strongly favor righties:

… and those who favor lefties:

For those who favored lefties the most, the large differential is due primarily to the fact that the hitter is exceptional against LHPs, and merely mortal against righties. Among those who favored righties, however, four - Justice, Javier, Goodwin and Anderson - had significantly lower K_zonelh than the league average. K_zone, when combined with K_zone pd, gives a useful assessment of whether a player should be platooned: when K_zone pd is high, and either K_zonerh (K_zone vs. righties) or K_zonelh is below 100, especially if significant, the option of platooning the player should be explored. None of the aforementioned four hitters should have batted against a lefty in 1998.

What about team ratings?

By taking all players who fit the subset criterion, grouping them by 1998 team, and weighting their overall eye ratings by plate appearances, we can come up with weighted average eye ratings for individual teams.

In 1998, this yields:

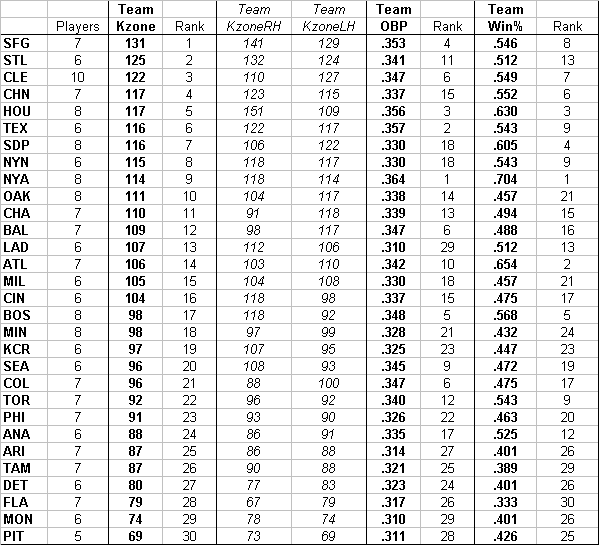
San Francisco had the best overall K_zone by far, led by Bonds, Javier, Mueller and Snow. St. Louis, in 2nd, were paced by McGwire, Deshields, Lankford, and Gant... the 3rd-ranked Indians by Giles, Lofton, Cora, Thome, Justice, Vizquel, and Ramirez.

What does K_zone say about a team's ability to win?

By performing regression analysis on the relationships of the different rankings above, we obtain the following:

OBA and K_zoneexplain by themselves about 50% of a team's ranking in Win%, a proxy for winning ballgames. The two factors together explain more than 60%.

Who said baseball was 75%+ pitching?

Conclusion…

If K_zone is a meaningful tool, then it must be true that BA and K_zone together explain most of OBA. The relevant regression produces an R² of 85.6%, satisfying the condition.

K_zone may not revolutionize the way the sport looks at statistics, or the way agents negotiate contracts, or the way teams, in general, approach the game. What it does do is give us a new way to isolate and examine one particular critical aspect of a hitter's game: his strikezone judgment. What we have shown here is that a high-OBA, high kzone team has, ceteris parabis, a statistically high probability of winning than a low OBA, low kzone team. The rating can also be used effectively to judge individual players.

It is my belief, although I haven’t yet attempted a proof, that a further study of kzone would reveal a strong positive correlation with career longevity. You will no doubt have noted from the tables herein that just about every player who ranks highly in K_zone is a mature, established hitter. My guess would be that those hitters who develop and maintain consistently high K_zone, especially in the early years of a career, are those who enjoy the most productive, and hence the longest, careers. Hitters like Matt Lawton, Chipper Jones, Scott Rolen and Brian Giles just may prove me correct.

TABLE - Top 50 by Aggregate K_zone (1998, 400+ PAs)

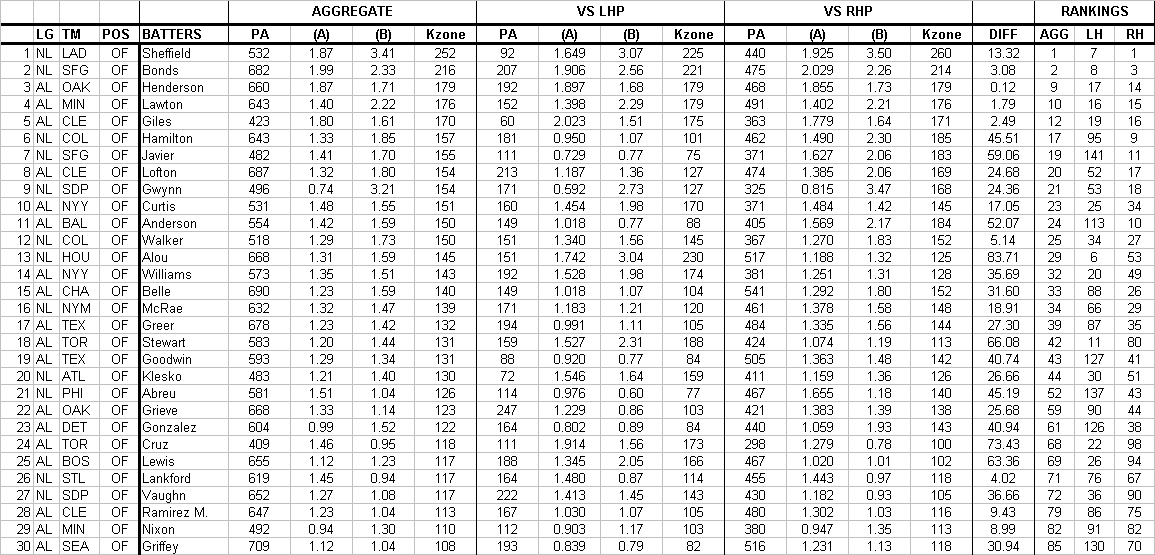
POSITIONAL K_zone: top K_zone by position.

Back to the top of page | BTF Essays Page| BTF Homepage | BaseballStuff.com