Deciphering the New Runs Created

by Jim Furtado with G. Jay Walker and Don Malcolm

[ Webmaster's Note: The following article appears in The 1999 Big Bad Baseball Annual. ]

You attended the gala celebration at its release. You watched people fight over it on Jerry Springer. You watched the two-hour Dateline special discussing its impact. You participated in focus groups that discussed its construct. But you're still thinking, "What does Bill James' new Runs Created (RC) formula actually do?"

OK, maybe none of this is true. Maybe you didn't fork out the $79.95 to read a little about it in either of the new STATS, Inc. books The All-Time Baseball Sourcebook or The All-Time Baseball Handbook. Maybe, just maybe, you haven't seen anything at all about the new RC. In any case, you still may be wondering what changes Bill James made to his creation and how it works. If so, read on.

The new RC—a big improvement ?

While the RC method is one of the seminal developments in sabermetric history, it soon became apparent that there was a problem with the original RC construct. Bill James himself commented on its deficiencies in his 1985 Baseball Abstract: “I’ve known for a little over a year that the runs created formula had a problem with players who combined high on-base percentages and high slugging percentages … The reasons that this happens is that the players’ individual totals do not occur in an individual context”. He went on to say, "I'll make some adjustments to the runs created formula within the next year or so. Right now, I don't know what they will be." That was fourteen years ago. If Bill intended to raise the level of anticipation for the changes, he certainly gave himself plenty of time.

Beyond the question of how much or little the new RC formula is an improvement over the old one, the work would have to be labeled a disappointment to many readers for the simple reason that Bill did not much explain his thought process behind the modifications, or for that matter even supply enough details so that others could easily replicate his work. He barely provided any justification for his changes themselves. Coming from the man who almost single-handedly broke the Elias monopoly on baseball information, it was disturbing to see him pitch his tent awfully close to those in the sabermetric community who fail to divulge the details of their methods or the thinking behind them in the name of propriety.

There is a rumor that Bill James will be releasing an update to his Historical Abstract sometime in 1999/2000. Maybe he figures he can explain the changes in more detail in the updated book. Without more information from Bill himself, we’re left to speculate. Speculate about how he came up with the changed formula. Speculate why he incorporated situational statistics. Speculate whyafter criticizing Pete Palmer for using actual runs in Linear Weightshe now factors actual runs into the revised formula.

Rather than just make wild guesses, however, we undertook an involved examination of the new RC methodology, and then spent a lot of time discussing among ourselves the possible reasons behind the changes. Of course, we didn't always agree. That happens when people are put in the position to guess what someone else is thinking.

How is the new RC calculated?

We'll run through the new RC calculations using Ken Griffey's 1998 statistics as an example. This is appropriate because Bill James used Ken Griffey's 1997 stats for the descriptions in both of the new stats books. The big difference between James’ description and this one is that we’ll fully explain the parts he glossed over. We'll also comment on the changes.

Step 1 - Calculate the A, B and C Factors

Figured just about the same way as James' classic tech version of the formula. The only difference is that James changes some of the terms depending on the availability of the data and the time period of the season in question. For the current time period (1988 to present), the Historical Data Group (HDG) 24 formula is used.

Calculate the A, B, and C terms as follows:

A = (H+ BB + HP - GIDP - CS)

B = [ TB + ((BB + HB - IBB)*.24) + (SB*.62) + ((SH + SF)*.5)-(SO*.03) ]

C = (AB + BB + HB + SH + SF)

For Ken Griffey Jr.:

A = (180 + 76 + 7 - 14 - 5)=244

B = ( 387 + (( 76 + 7 - 11) * .24) + (20 * .62) + (( 0 + 4)*.5) + ( 121*-.03))=415.05

C = (633 + 76 + 7 + 0 + 4)=720

If things were still calculated the classic way, we'd simply calculate Griffey's RC by A*B / C. This would give us what I call Griffey's "base H24". Putting the numbers together would give us 140.66 RC.

What Does this Do?- This is the classic RC construct with a couple of minor changes. James slightly modified the "B" term. For comparison, the classic Tech-1 version's B factor looked like this: (TB+((BB+HBP-IBB)*.26)+((SF+SH+SB)*.52)). James also splintered SB off from SF+SH and then slightly changed the coefficient. The biggest change to this part of the calculation, however, was the addition of a term for strikeouts. This is an area of great debate among sabermetricians. My own research agrees with this adjustment. I found that although the difference between regular outs and strikeouts is rather small (-.008 for Extrapolated Runs), it is nonetheless something that should be included in run estimation formulas.

Step 2 - Calculate initial Runs Created (iRC) by inserting A, B, and C factors into theoretical team context and round off the result:

iRC = [ ((A + (2.4*C)) * (B + (3*C)))/ (9*C) ] - .9 * C

Griffey iRC = [ ((244+ (2.4*720)) * (415.05 + (3*720)))/ (9*720) ] - .9 * 720=135.64 or 136 iRC

Two additional things that happen here is 1) iRC gets rounded into a whole number 2) any negative results for individual players get changed to 0.

What Does this Do? -This has been one of the most talked about changes to the new RC. Bill James describes this step as, "The runs created for each individual are now figured in a "theoretical team" context, rather that assuming, as I did before, that an individual's offensive contributions interacted with one another. " What do we think? Well, I had yet to hook up with the BBBA guys when the changes were made public, so while I was trying to decipher this step on the East Coast, Jay Walker was doing the same thing on the West Coast. In hindsight, that was a very good thing. Why? Because Jay and I took slightly different looks at this construct and came to different conclusions. Jay looked at the new construct and tried thinking along with Bill James. I looked at the construct and tried to see if I could separate the formula into two distinct parts: 1) the original A*B/C construct and 2) a kludge factor. The interesting thing, though, is that both of our conclusions were correct.

Jay's Take

What did Jay come up with? He came up with two expressions, Part 1 and Part 2.

Part 1 - ((A + 8*.300*C) * (B + 8*.375*C)) / (9*C)

Part 2 - ((8*.300*C) * (8*.375*C)) / (8*C)

Subtracting Part 2 from Part 1 not only gives the same results as James’ calculation, but it can be shown algebraically that it is in fact James’ equation, merely expressed in a different way.

With a bit of scrutiny of these two expressions, it becomes fairly obvious what Bill was trying to do. For simplicity, let’s call Factor A, the on-base factor, which is similar to, but slightly different from the on-base average. In a similar manner, we’ll call Factor B the slugging factor and Factor C the plate appearance factor. For his team context, Bill assumes you’re on some sort of team with eight other players, and each of these eight players has an on-base factor of .300 and a slugging factor of .375. The Part 2 expression above is equal to the number of runs created that this team of eight players would produce, assuming each had the same number of plate appearances as you did. The Part 1 expression is the number of runs created that this team of eight players would produce with you added to the team. Subtract Part 2 from Part 1, and you get the number of runs created the team produces with you, minus the number they produce without you. The result is the runs that you create while in a team context.

While this is a fairly innovative technique, it also begs a number of questions. First, how were the .300 and .375 factors derived? What kind of analysis went into deciding that these were the numbers to use? And given the preciseness of the coefficients in the various RC formulas, why are these numbers so rounded off? Might something like .302 and .374 be better choices? Or did .300 and .375 just happen to be the best? Second, what exactly do the .300 and .375 represent? Are the meant to be the numbers for an average team, a replacement team or something in between? Third, why are the .300 and .375 applied globally across all eras? Surely a representative on-base factor and slugging factor have varied over time? Or has this change over time already been factored into the coefficients of the RC formulas? Finally, why one could well imagine the Bill James of the 1980s presenting his formula in an understandable manner and explaining what it does and how it was derived, why does the Bill James of the late 90s camouflage his formula in such a way as to make his methods and purposes incomprehensible to most of his readers?

Jim's Take

As I mentioned above I looked at the formula and came up with a different view of the calculation. My algebraic manipulations led to this:

[ 1/9* ((A*B)/C) ] + [ A/3 + 0.8*B/3 - 0.1*C ]

Admittedly, this doesn't look that interesting at first glance. The bracketed part is the classic RC formula multiplied by 1/9. The second bracketed doesn't look like it makes much sense when I first examined it, but finally, it hit me. The second part is really just a linear formula dressed up in unfamiliar clothing. If you take the time to break it down like I did, you'll find that the second part equals (for Historical Data Group 24):

8/9 * [.5625*1B +.8625*2B +1.1625*3B + 1.4625*HR + .3345*(BB+HP-IBB) + .2625*IBB +.186*SB - .375*(CS+DP) +.0375*(SH+SF) -.1125*(AB-H-SO) - .1215*SO]

So the second part is really just 8/9th times a linear formula, which looks a lot like the Extrapolated Runs formula with different coefficients. What all this essentially means is that Bill James' new "team construct" is really just 1/9th of the classic Runs Created plus 8/9th of a linear formula. So in one sense you could say that since Bill is already up to his neck in the linear pool, he might as well get his hair wet. What’s interesting is that he had previously stated when talking about Paul Johnson's Estimated Runs linear formula, “…there probably are compromises between the two methods that will prove to be yet more accurate than either method”.

While I agree that the “West Coast” version accurately reflects Bill James’ intentions in developing his team adjustment, my discovery is still very interesting. Bill James' work has led him to calculate player RC values that are 89% linear. This change has greatly increased the accuracy of RC on the player level. However, it still doesn't make them as accurate as Extrapolated Runs, a 100% American-made linear formula.

Step 3 - Calculate the adjustment for home runs with runners on base

The first situational adjustment in the new RC method is made for how many home runs Griffey Jr. hits with runners on base. This is another adjustment that Bill James didn't fully explain. We need four bits of information for Griffey to do this adjustment:

Total AB = 633
AB with runners on base = 303
Total HR = 56
HR with runners on base = 26

Then calculate how many HRs Griffey would be expected to hit with runners on base, proportional to his AB.

Expected HRs = (303/633*56) = 26.81

Subtract Expected HR from actual HR with runners on base and round the result

26 - 26.81 = -.81 or -1

This leaves Griffey with an adjustment for home runs with runners on base (HR-ROB) of -1.

Step 4 - Calculate the adjustment for batting average with runners in scoring position

The information we need here is Griffey's regular batting average and his batting average with runners in scoring position. It’s suggested you carry out this calculation to an extra decimal place.

Regular Batting = 180 hits / 633 at bats or .2844

Batting with runners in scoring position = 57 hits / 184 at bats or .3098

Subtract regular batting from batting with runners in scoring position, multiply the result times at bats with runners in scoring position, and round the result.

(.3098-.2844)*184 = 4.674 or 5

This gives Griffey an adjustment for batting with runners in scoring position (AvgSP) or +5

What Does this Do? – whether or not to use situational stats is a point that has been debated by sabermetricians for years. Bill James’ introduction of situational stats represents a major philosophical departure from anything he’s previously done with his RC methods. The only justification he gives for now using situational stats is that their use “substantially reduces the standard error of team runs created estimates”. This seems close to becoming his sole criteria for deciding what does and doesn’t get included in the RC methodology.

This issue of whether to use situational stats really boils down to all the old arguments about clutch hitting. Does it exist? If it does, then why do some players hit better in the clutch? For those that do, does laziness or attitude cause them to perform less well in routine situations? And if so, how valuable are they really? There was a time when Bill expressed serious doubts about whether clutch hitters really existed, or if good and poor clutch hitting performances merely represented random fluctuations.

Regardless of his reasons for deciding to take his RC method down the situational path, James’ choice of clutch-hitting stats, or in particular, his selection of the homers with runners on base stat, is curious. For any given player, that stat is highly dependent on the ability of the teammates who bat before him in the batting order to get on base. This introduces a whole subjective element to the RC method. If James chose not to use runs or RBIs in previous versions of the RC methodology because of their subjective nature, why is he now bringing in these subjective stats?

There is no absolute truth about whether situational stats should be used in measuring offensive performance. However, there are certain questions to consider. They tie-in with the whole idea of framing a question properly and then choosing the proper methodology to answer that question. The original RC was the foundation of the answer to the "Who's best?" question. RC estimated the number of runs a player would create in a standard context. Although this context included park effects, James' later accounted for them by the Offensive Winning Percentage component of his evaluation method. The end result of his full method was a context free comparison of players.

Is James trying to answer a different question with his new RC methodology? If so, which one? It doesn't really answer the "Who's best?" question anymore with the inclusion of his situational stats plus a reconciliation step (discussed later), which introduce a subjective bias. Is he trying to answer the "Who's most valuable” question? Bill leaves us no clue as to what was behind this major philosophical switch, only that he wanted to “substantially reduce(s) the standard error of team runs created estimates”. Maybe that’s all there was—we don’t know.

Step 5 - Calculate the Preliminary RC (PrelimRC)

Add together Griffey's initial Runs Created total with the situational adjustments to get his preliminary RC:

PrelimRC = iRC + HR-ROB + AvgSP

PrelimRC = 136 - 1 + 5 = 140

What Does this Do? – this step is rudimentary, other than to note that if you’re in the camp that desires to have a context-free measure of offense, this contaminates it with situational adjustments.

Step 6 - Calculate the team reconciliation factor

After calculating PrelimRC for all players, sum all the rounded individual players' PrelimRC.

The 1998 Mariners PrelimRCs add up to 892 PrelimRC.

Divide the actual team runs (859) by the team PrelimRC (892) to calculate reconciliation factor (RF):

1998 Mariners RF = 859 / 892 = .963

?What Does this Do? – if reducing the standard error of team runs created estimates is to your mind the only way to measure the worth of your offensive performance measure, then this becomes the perfect solution . Just reconcile the RC values of all the players on the team to the number of runs scored by the team and voila!–your standard error estimates are all reduced to zero. Can’t do much better than that. If the glove doesn’t fit, just plain force it.

This can be regarded as pretty much of a copout, an attempt to get all your numbers to balance, to reduce your error percentage and to try and skirt around the inadequacies of the model.

One of my sons once used a similar approach to solve a very different problem. Unable to find a pentagon-shaped hole on his toy, my son tried to use a toy hammer to force the pentagon-shaped peg into a round hole. When I saw him trying to do this, I spent a little time showing him why this wasn't a good idea. Of course, I can understand why he tried to fit it with his hammer. The shapes were pretty much the same. After looking over the other holes on the ball, he decided the circle hole was the only possible place to insert the ball. When it didn't fit quite right, he gave it a little help with his hammer. In his mind, this was the only available option.

Unfortunately, this appears to be the same conclusion Bill came up with. The BBBA crew and I prefer a different course. We'll keep looking for the right hole.

Step 7 - Multiply team reconciliation factor times individual player's PrelimRC and round off to get the final RC result:

For Griffey, 140 PrelimRC * .963 = 134.82 or 135 Runs Created for 1998.

?What Does this Do? – beyond our criticism of this method to force your run estimates to match the actual runs score, the application of the method introduces all kinds of subjective biases to your results. The 1998 Mariners had a 33-run shortfall between their runs scored and their summed up RC estimates. Who’s to say how this shortfall should be distributed? Griffey absorbs 5 runs of the 33-run shortfall? Even if you believe you have to stick this shortfall on someone (and we don’t) who’s to say whether Griffey shouldn’t instead absorb 10 runs of the shortfall? Or maybe Griffey should actually be credited with 2 additional RC and his teammates be left to absorb a 35-run shortfall instead of the 33 runs. It’s all a guessing game. Read on…

Reconciliation or incorporating the error for teams into player values?

Does new theoretical team context do what it's supposed to?

The team reconciliation process done in Steps 6 and 7 is the part of James' changes that we question the most. Here's what Bill James has to say about this part of the process:

"Finally, we reconciled runs created, after the fact, with the runs actually scored by the team. Suppose, for example, that the individual runs created estimates for the members of a team were to total up to 500, but the team actually scored 700 runs. This would be an extraordinary thing, and I don't think such a discrepancy has ever actually happened. We're ordinarily talking about an adjustment in the range of 20 runs per team, or two runs per player. But if it did happen, we would then increase the runs created for each individual on the team by 40%, since 700 divided by 500 is 1.4. We don't know who created these extra runs, but somebody on the team certainly did. The best we can do is distribute them among the hitters proportional to their accomplishments."

Is Bill correct about the error rate of the formula? Well, the average absolute error for all teams from 1984-1987 is about 20 runs. The range of errors is a much broader however.

The biggest error for the formula during that time period is the +74 error for the 1987 Cubs. Since the Cubs scored 720 runs that season and the formula projects 794 runs, the formula overestimates by 10.2%. Who does the team reconciliation affect the most? Andre Dawson. Dawson loses 10 runs to "reconciliation". Instead of being credited with 110 runs, "The Hawk" gets credit for only 100.

Is this really fair? Did Andre's play generate less than the 110 runs the formula estimates? We don't know for sure, so it's not fair to penalize him. What's the point? Does subtracting the ten runs tell us something about Andre Dawson? No. The fact that the formula overestimates tells us that his team was less efficient than an average team, not that Andre was less efficient.

To further illustrate, let's look at the other extreme from the same season. The largest negative error for the 1987 National League belonged to the Cardinals. The Cardinals scored 798 runs enroute to the 1987 World Series title, while the Cardinal players are estimated to have 755 RC, an error of -43 runs. To account for this discrepancy 43 runs must be added to the player totals.

Which player benefits the most from this largesse? Jack Clark. Clark gets credited with 124 runs instead of 117 runs. Again, is this fair? No. The fact that the formula underestimates tells us that Clark's team was more efficient than the average team, not that Jack was more efficient.

The end result of this "reconciliation" is that Jack Clark ends up with 24 more runs created than Andre Dawson. Compare this to the original difference of 7 runs (Dawson 110, Clark 117). The spread between the players is widened. Unfortunately this is due to the inaccuracy of the formula, not due to any quantifiable difference between them.

Remember we're looking for objective evidence. Is this so much different from looking at the numbers and fiddling with them? Another subjective method to divvy up the extra runs could be to guess who generated the runs. I could say, "Jack Clark is so awesome with all those slap-hitting single hitters around him, he must have created more runs than 117. Give him the extra 23 runs. He's the best!" Or I could base my reconciliation on the number of plate appearances. Is James' reconciliation really much different? Essentially what he says is that if a player accounts for 10% of the RC projection, then the player creates 10% of run overestimate or shortfall. It’s just one of a number of subjective criteria that could be applied.

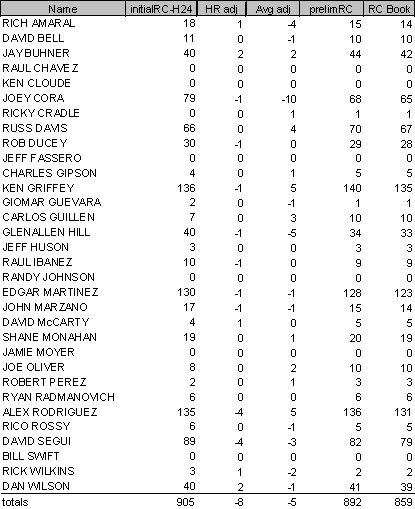
This problem is compounded when the situational adjustments are factored in. To illustrate, I present the data from the 1998 Seattle Mariners and the 1998 Oakland Athletics.

1998 Seattle Mariners

1998 Oakland Athletics

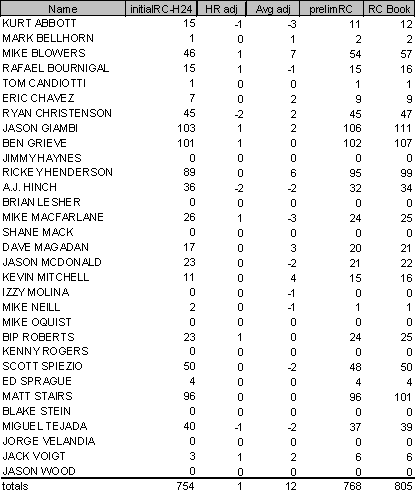
The reason I chose these two teams is simple, they are the teams who had the "actual run hammer" applied hardest. Seattle scored 859 runs in 1998, while team RC-H24 predicts 906 runs; Oakland scored 804 runs in 1998, while team RC-H24 predicts 752 runs.

Although the team RC is only slightly different than the summed individual player totals (Sea 906/905 and Oak 752/754), the difference between the PrelimRC totals and actual runs is still substantial. Seattle's team estimate over-projects by 32 runs, while Oakland's team estimate under-projects by 37 runs. The end result of the hammer application is that Ken Griffey loses 5 runs and Ben Grieve gains 5 runs due to nothing other than the inadequacies of the formula.

Moving on to inspecting the situational adjustments, notice that these adjustments can have considerable affect on player totals. Rickey Henderson gains 6 runs due the adjustment, while Joe Cora loses 11 runs. Is Rickey really a great clutch hitter? Is Joey Cora a bad one? How about Alex Rodriguez, what conclusion can we draw from his adjustments? Even though Alex's minus 4 HR adjustment would lead us to believe he doesn't hit so well in the clutch, his plus 5 Batting Average adjustment would lead us to believe he does. Without looking into the reasons a team's estimate over/under projects, it just becomes a guessing game as to who is responsible for an offense being more or less efficient. As Jay once commented to me: "When all is said and done, the situational adjustment and team reconciliation steps obfuscate more than clarify player analysis."

As Harry Chadwick was the premier baseball analyst of the 19th century, Bill James can probably lay as much claim as anyone to being the leading analyst of the 20th century. The BBBA staff and myself are admirers of a great deal of his work. Unfortunately, his New RC reminds us a lot of the New Coke. Although the New RC was supposed to be an improvement, like the New Coke, it's really just different. And like the New Coke, we don't like the way it tastes.

Back to the top of page | BTF Homepage | BBBA Web Site